Gaussian processes are revolutionizing the world of quantum machine learning by providing a novel, efficient, and mathematically grounded approach for quantum computers to learn from data. This development is exciting because it overcomes major roadblocks that previous quantum neural networks encountered, promising a smoother path to harnessing quantum computing’s power for solving complex problems beyond classical capacities.

If you’ve ever wondered how computers “learn” — whether it’s a self-driving car recognizing pedestrians or AI translating languages — you’ve encountered classical machine learning, often powered by structures called neural networks. Quantum computing, a new type of computing that uses the principles of quantum physics, aims to do this learning even faster and for problems classical computers cannot easily solve.
But how do Gaussian processes fit into this exciting frontier?
Table of Contents
Gaussian Processes Provide a New Path Toward Quantum Machine Learning
| Topic | Details |
|---|---|
| What are Gaussian processes? | A probabilistic method modeling data with bell-curve distributions, useful for predictions. |
| Quantum advantage | Overcomes “barren plateau” problems in quantum neural networks, leading to more efficient learning on quantum devices. |
| Research breakthrough | Los Alamos National Laboratory proved genuine quantum Gaussian processes exist and are effective. |
| Applications | Quantum regression, Bayesian optimization, adaptive predictions on quantum data. |
| Key sources | Los Alamos National Laboratory, Nature Physics |
Gaussian processes offer a fresh and promising pathway in the quest for practical quantum machine learning. By leveraging their well-founded Bayesian nature and avoiding the pitfalls of quantum neural networks, quantum Gaussian processes stand poised to unlock the full potential of quantum computers in learning from data. Whether you are a researcher, a student, or a tech enthusiast, understanding this new approach will keep you ahead in one of the most exciting technological frontiers.
What Are Gaussian Processes?
Imagine you want to predict tomorrow’s temperature based on a few days’ data. Instead of guessing one exact number, how about saying, “there’s a high chance it’ll be around 25°C, but maybe a bit warmer or cooler”? This way of predicting, with some built-in uncertainty, is exactly what Gaussian processes (GPs) do. They model data not as fixed points but as distributions, often bell-shaped curves (hence “Gaussian”), which tell us probable outcomes with confidence intervals.
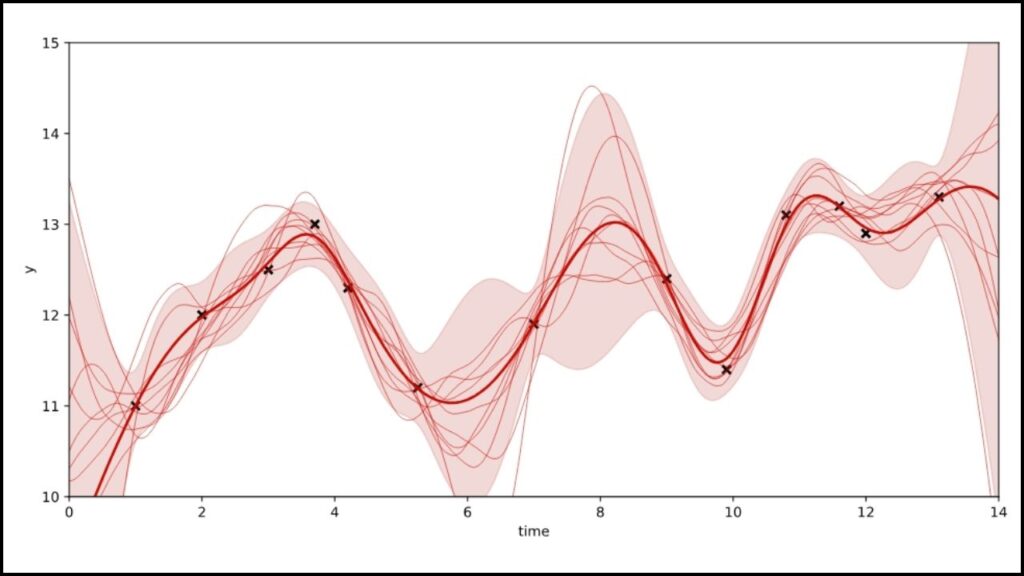
In classical machine learning, Gaussian processes are prized for their non-parametric, Bayesian nature. Non-parametric means they don’t rely on preset numbers of parameters—they grow as they get more data. Bayesian means they update predictions as new data comes in, becoming smarter over time.
From Classical to Quantum: Why the Leap Matters
Quantum computers work fundamentally differently from classical ones. They process information using qubits, which can represent complex probabilities and superposed states, enabling them to solve certain problems much faster than classical computers.

For years, scientists tried to replicate the power of classical neural networks—widely used for complex tasks—in quantum environments. However, they ran into a notorious issue called “barren plateaus”: as quantum neural networks grow, their learning gradients vanish, making it almost impossible to train them effectively.
A team of quantum computing researchers at Los Alamos National Laboratory decided to rethink the approach. Instead of directly copying neural networks, they asked: What if we use Gaussian processes, known for their simpler and more robust mathematical foundation, in quantum systems? Their work led to a breakthrough by proving genuine quantum Gaussian processes can exist and be harnessed for efficient quantum machine learning.
How Do Quantum Gaussian Processes Work?
In classical machine learning, large neural networks have been shown to converge to Gaussian processes. This means that when you have enough neurons, the network’s output starts behaving like a Gaussian process. The Los Alamos team demonstrated a similar phenomenon applies for quantum neural networks, where the output of certain quantum circuits converges to a quantum analog of a Gaussian process.
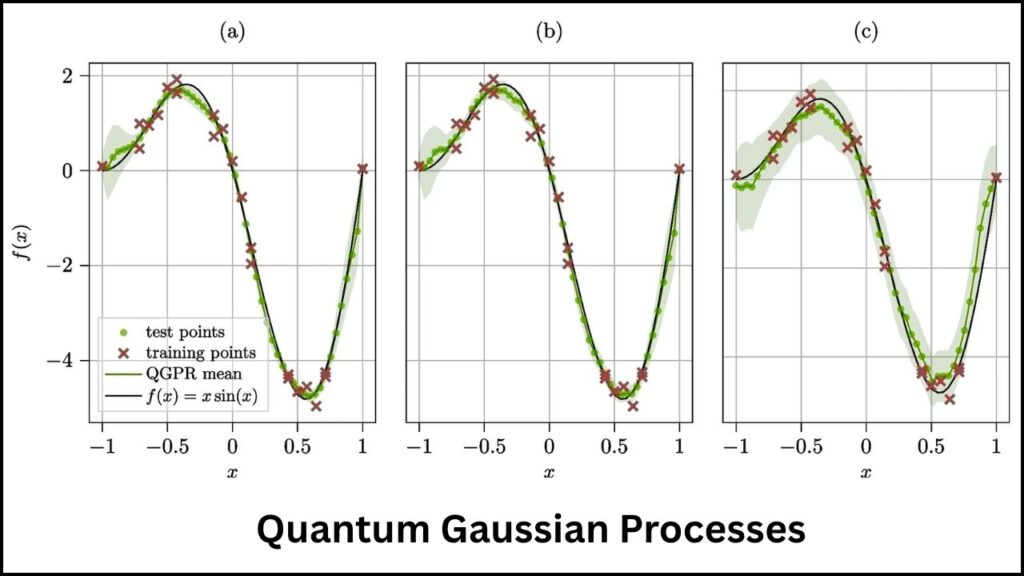
This has major implications:
- It means quantum machine learning can leverage Bayesian inference for learning, which is well-understood and mathematically robust.
- It sidesteps the issues of barren plateaus by not requiring heavy parameter tuning or training.
- It supports quantum regression tasks and Bayesian optimization, essential for making predictions and optimizing quantum circuits respectively.
Practical Examples and Applications
- Bayesian Optimization on Quantum Devices:
Using quantum Gaussian processes, scientists can optimize parameters of quantum circuits faster. This translates into better and more efficient quantum computations, which are crucial for tasks like drug discovery or materials science. - Adaptive Learning in Quantum Systems:
Because Gaussian processes handle uncertainty well, quantum systems can better adapt predictions as new quantum measurement data arrives, making quantum algorithms more robust. - Classical-Quantum Hybrid Models:
Hybrid algorithms combine classical computing with quantum Gaussian processes for efficient training and execution, leveraging the strengths of both worlds.
Step-by-Step Guide: Getting Started with Quantum Gaussian Processes
- Understand Classical Gaussian Processes:
Start by learning basics—how GPs model data as distributions, and how they perform regression and update predictions. - Explore Quantum Computing Fundamentals:
Learn about qubits, quantum gates, and how quantum circuits differ from classical algorithms. - Study Quantum Neural Networks:
Get familiar with variational quantum circuits and the concept of barren plateaus. - Dive into Quantum Gaussian Processes:
Review recent research (e.g., Los Alamos team’s findings published in Nature Physics) that prove quantum GPs’ existence and functionality. - Experiment with Simulators:
Use quantum computing frameworks like IBM’s Qiskit or Google Cirq to simulate quantum Gaussian process algorithms. - Apply to Real Quantum Data:
Use quantum GPs to fit and predict outcomes on datasets, practicing Bayesian updates and optimization.
Scientists Just Found a Way to Reverse Time and Erase Mistakes: The Quantum Breakthrough Explained
A Quantum Computer From Just One Wire? Scientists Say It’s Possible
Scientists Trigger a Wild Quantum Switch in Exotic Material — Superconductivity Breaks the Rules
FAQs About Gaussian Processes Provide a New Path Toward Quantum Machine Learning
Q1: How do Gaussian processes differ from neural networks?
Gaussian processes do not assume a fixed number of parameters and model uncertainty directly, while neural networks use fixed layers of neurons and require training to adjust weights.
Q2: What is the “barren plateau” problem in quantum neural networks?
It refers to a difficulty where the gradient signals needed to train quantum neural networks become vanishingly small as system size grows, stopping effective learning.
Q3: Why are Gaussian processes better for quantum machine learning?
Because they avoid issues like barren plateaus by being non-parametric and allow for efficient Bayesian inference directly on quantum data.
Q4: Can quantum Gaussian processes run on today’s quantum computers?
Current quantum hardware is still noisy and limited, but simulations and early experiments show promise. As quantum technology matures, quantum Gaussian processes will become more practical.