New Quantum Glasses: Quantum computing is on the brink of a revolution, but one major challenge stands in the way: quantum error correction. In June 2025, scientists unveiled a breakthrough approach using “quantum glasses”—a concept inspired by physics—that could finally unlock optimal error correction codes, making quantum computers far more stable and reliable than ever before. This article explores what this means, how it works, and why it matters for the future of technology.
New Quantum Glasses
| Feature/Fact | Details & Data |
|---|---|
| Breakthrough | PLANAR algorithm enables exact, optimal decoding for repetition codes under circuit-level noise |
| Error Rate Reduction | Achieved a 25% reduction in logical error rates in Google Quantum AI’s experimental data |
| Quantum Error Correction (QEC) | Essential for making quantum computers scalable and reliable |
| Practical Impact | Reveals that many errors previously blamed on hardware are actually due to suboptimal decoding |
| Career/Professional Relevance | Opens new research and engineering roles in quantum error correction, algorithm development |
| Official Resource | Google Quantum AI |
The discovery of quantum glasses and the development of the PLANAR algorithm mark a significant leap forward in quantum error correction. By achieving optimal decoding for repetition codes and slashing logical error rates, this innovation brings us closer to the dream of stable, scalable quantum computers. The impact will be felt across research, industry, and education, opening new possibilities for technology and science.
What Is Quantum Error Correction and Why Is It So Important?
Quantum computers use qubits—the quantum version of classical bits. Unlike regular bits, qubits can exist in a superposition of 0 and 1 at the same time. This property gives quantum computers their incredible power, but also makes them extremely sensitive to errors from their environment, such as:
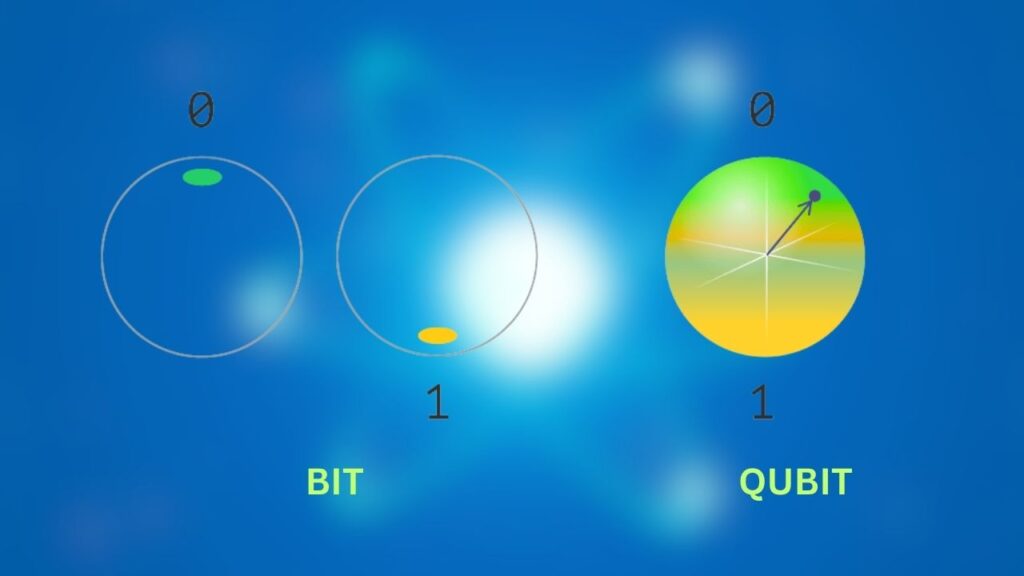
- Decoherence: When a qubit loses its quantum state due to interference from the outside world.
- Gate errors: Mistakes when performing quantum operations.
- Measurement errors: Reading the wrong value from a qubit.
Even a tiny error can ruin a complex quantum calculation. That’s why quantum error correction (QEC) is considered the backbone of practical quantum computing. Without it, quantum computers would be too unreliable for real-world use.
How Does Quantum Error Correction Work?
At its core, QEC spreads information across multiple qubits, so that if one or a few go wrong, the original information can still be recovered. This is similar to how classical computers use error-correcting codes, but with extra challenges:
- No-cloning theorem: You cannot make perfect copies of an unknown quantum state.
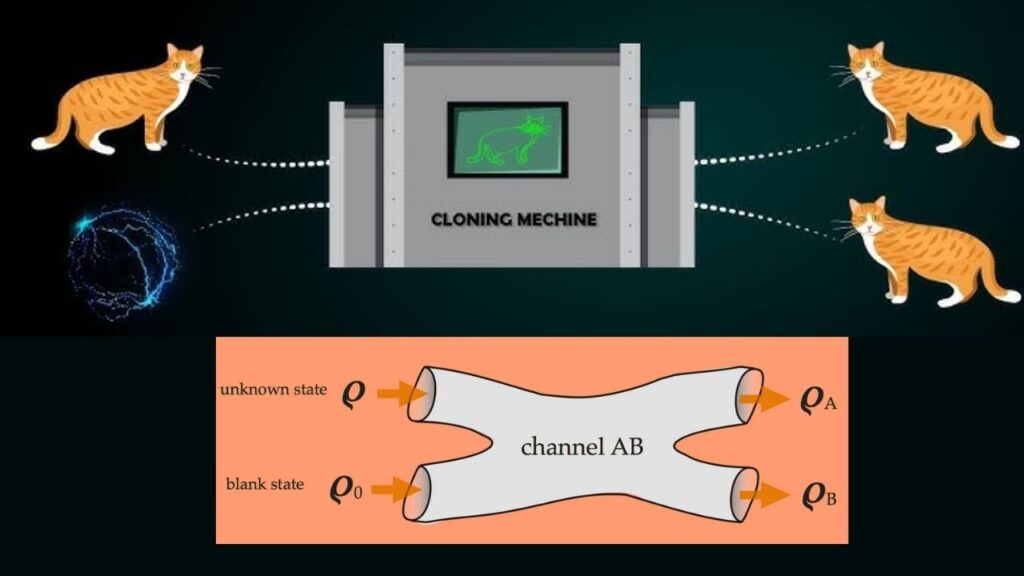
- Measurement destroys state: Measuring a qubit usually erases its quantum information.
- Multiple error types: Qubits can suffer not just from bit flips (0 ↔ 1), but also phase flips and more gradual errors.
To overcome these, QEC uses clever encoding, partial measurements (called syndrome measurements), and correction steps to keep quantum information safe.
The Role of Repetition Codes and Decoding
One of the simplest QEC strategies is the repetition code. Imagine you want to store a single bit of information. In classical error correction, you might copy it three times: 1-1-1. If one bit flips, you can use a majority vote to guess the original value.
Quantum repetition codes work similarly, but with extra tricks to handle quantum rules. However, decoding—the process of figuring out what errors happened and how to fix them—can be very tricky. The most common decoding method, called minimum-weight perfect matching (MWPM), is fast but not always optimal, sometimes introducing its own errors.
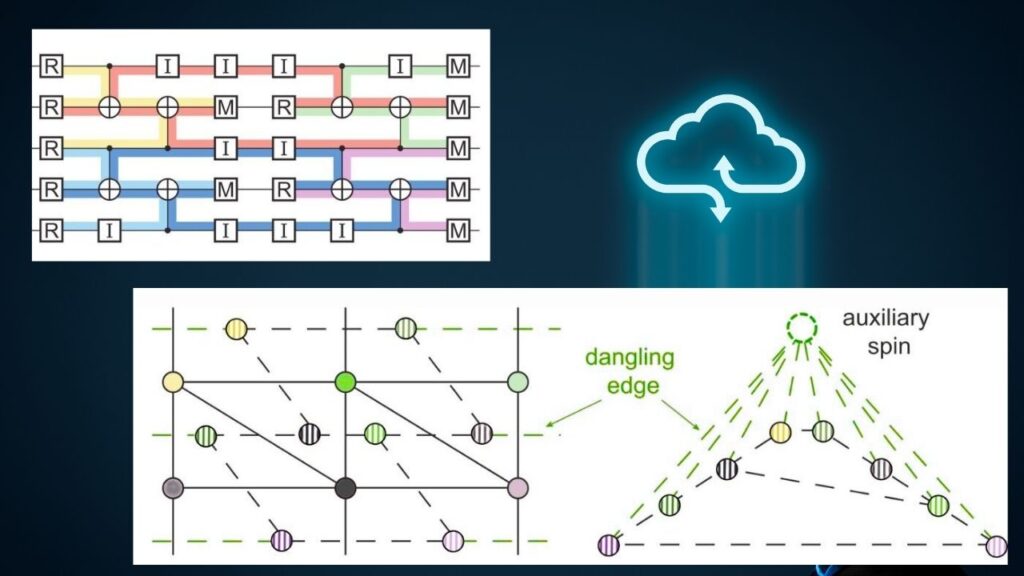
The Quantum Glasses Breakthrough: PLANAR Algorithm
So, what’s new in 2025? Scientists discovered that the mathematical structure of certain quantum error correction codes—specifically, repetition codes under circuit-level noise—resembles a type of disordered physical system called a spin glass. By applying insights from physics, they developed the PLANAR algorithm, which can find the exact best way to decode errors.
What Makes PLANAR Special?
- Optimal Decoding: Unlike MWPM, PLANAR always finds the best solution for repetition codes, eliminating algorithmic errors.
- Major Error Rate Reduction: When tested on Google Quantum AI’s data, PLANAR cut logical error rates by 25%, showing that many errors were due to the old decoding method—not the hardware itself.
- Scalability: Repetition codes can now be used more effectively for benchmarking and scaling up quantum computers, reaching error rates as low as 10−1010−10.
Why Does This Matter for Quantum Computing?

For Researchers and Engineers
- Better Benchmarking: PLANAR helps distinguish between hardware errors and algorithmic errors, allowing researchers to focus on real hardware improvements.
- New Algorithms: The approach opens the door to developing similar optimal decoders for more complex codes, like surface codes, which are widely used in quantum hardware.
- Career Opportunities: There’s growing demand for experts in quantum error correction, quantum algorithms, and quantum hardware engineering.
For Industry and Society
- More Reliable Quantum Computers: Lower error rates mean quantum computers can tackle bigger, more complex problems in chemistry, finance, and cryptography.
- Cost Efficiency: Optimal error correction could reduce the number of physical qubits needed, making large-scale quantum computers more affordable.
For Students and Beginners
- Easier to Learn: The PLANAR algorithm and its connection to spin glasses provide a clear, physical analogy that helps demystify quantum error correction for newcomers.
Step-by-Step Guide: How Quantum Error Correction Works
1. Encoding
- The quantum information (a logical qubit) is spread across several physical qubits using a code like the repetition code or surface code.
2. Error Detection
- Special helper qubits (ancilla) interact with the data qubits to measure syndromes—signals that reveal where errors have likely occurred.
3. Decoding
- The syndromes are analyzed using algorithms (like MWPM or PLANAR) to deduce the most probable error pattern.
4. Correction
- The identified errors are reversed by applying quantum operations, restoring the logical qubit to its intended state.
5. Decoding (Final Step)
- The logical qubit is extracted from the group of physical qubits, ready for use in further computation or measurement.
Tiny Nanoneedle Cancer-Detection Patch May Replace Painful Biopsies
Summer Solstice 2025 Marks Official Start Of Northern‑Hemisphere Summer
Cold Spray 3D‑Printing Technique Proves Effective For On‑Site Bridge Repair
FAQs About New Quantum Glasses
What are quantum glasses?
Quantum glasses refer to the mathematical analogy between error patterns in quantum codes and disordered systems called spin glasses in physics. This analogy helped scientists develop the PLANAR algorithm for optimal error correction.
Why is quantum error correction so hard?
Quantum error correction is challenging because quantum information can’t be copied, and measuring qubits usually destroys their state. Plus, there are more types of errors to handle compared to classical bits.
What is the difference between MWPM and PLANAR?
MWPM is a fast, widely-used decoding algorithm but is not always optimal, sometimes introducing extra errors. PLANAR, inspired by quantum glasses, finds the exact best solution for repetition codes, reducing logical error rates by 25% in experiments.
Will this make quantum computers available sooner?
This breakthrough removes a major barrier to scaling up quantum computers, but practical, large-scale quantum computers still require advances in hardware and other types of error correction codes.
Where can I learn more about quantum error correction?
You can find more details and updates on quantum error correction from the official Google Quantum AI project and other reputable quantum computing research institutions.