Quantum computing is often described as the future of technology, promising computers that can solve problems far beyond the reach of today’s fastest supercomputers. Among the many approaches to building such machines, topological quantum computing stands out for its built-in protection against errors. At the heart of this approach are exotic particles called anyons, which can store and process quantum information through a process known as braiding. However, until recently, braiding alone had a major limitation: it couldn’t achieve true universality when scaling to many qubits. That is where projective measurements come into play, unlocking a new level of power in quantum computing with anyon braiding.
A new study published in August 2025 by researchers Themba Hodge, Philipp Frey, and Stephan Rachel (arXiv preprint) demonstrates how combining braiding with projective measurements can restore universality and scalability to topological quantum computing. Their work offers fresh hope for building robust, large-scale quantum machines.
Table of Contents
Projective Measurements Unlock New Power in Quantum Computing With Anyon Braiding
| Aspect | Details |
|---|---|
| Study | Projective Measurements: Topological Quantum Computing with an Arbitrary Number of Qubits |
| Published | August 2025, arXiv |
| Key Idea | Combining anyon braiding with projective measurements restores universality in quantum computing |
| Demonstrated | Bell states (2 qubits), GHZ states (5 qubits), and scalable 10-qubit random circuits |
| Performance | Achieved >99% fidelity under moderate disorder |
| Applications | Fault-tolerant quantum computing, quantum simulations, advanced cryptography |
The discovery that projective measurements can unlock universality in topological quantum computing with anyon braiding marks a major step toward scalable, fault-tolerant quantum computers. By blending the robustness of braiding with the flexibility of measurement, researchers have charted a path to machines that could one day transform cryptography, medicine, finance, and beyond. The road to practical implementation is still long, but this breakthrough provides the blueprint for the future.
Understanding Anyons and Braiding
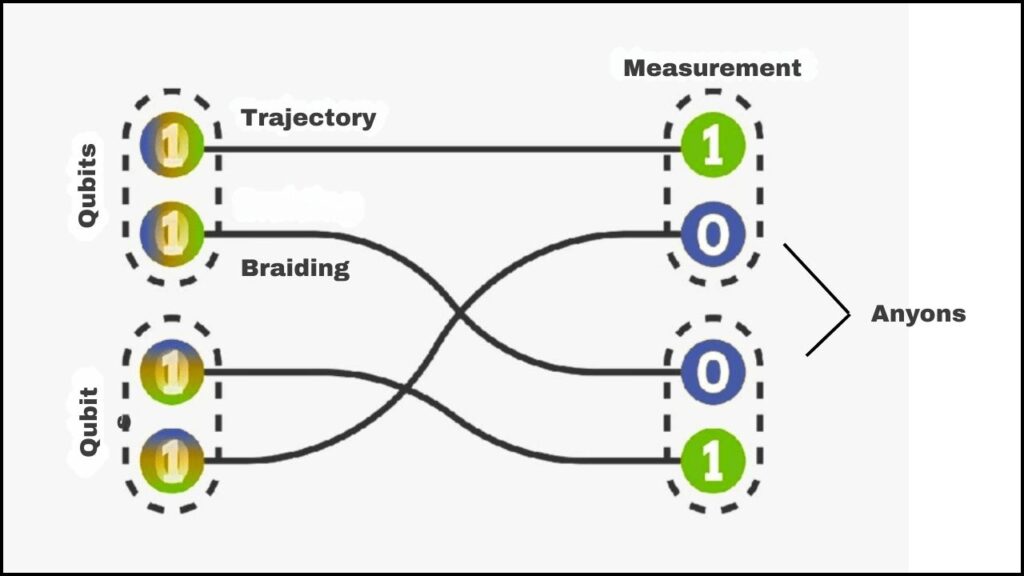
To appreciate why this research matters, let’s first break down the basics.
Most people are familiar with two types of particles: bosons (like photons) and fermions (like electrons). But in two-dimensional systems, a stranger particle type can emerge: anyons. Unlike bosons or fermions, anyons can have properties in between. What makes them especially fascinating is that when two anyons are exchanged or braided around each other, the system’s quantum state changes in a way that depends on the path taken — not just the start and end points.
This path-dependence gives anyon-based systems natural resistance to noise and errors, which is why topological quantum computing is considered one of the most promising error-proof models. However, braiding by itself cannot perform every possible quantum operation, limiting scalability beyond a couple of qubits.
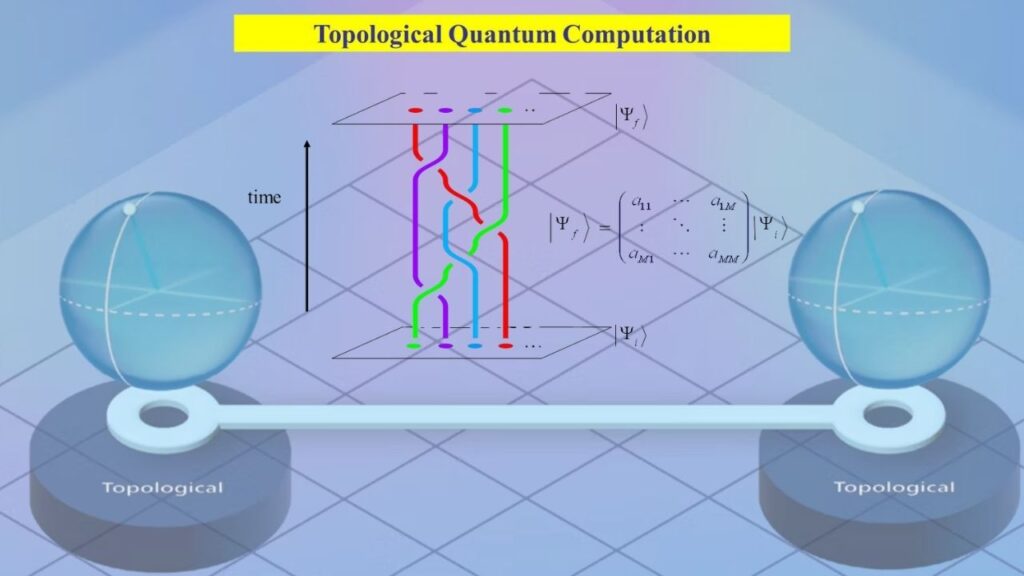
What Are Projective Measurements?
A projective measurement is a type of quantum measurement that collapses a system into one of its possible states. While measurement often destroys information in standard quantum computing, in this approach it becomes a tool for control.
By carefully choosing when and how to measure, researchers can switch between different qubit encodings.
This makes it possible to access operations that braiding alone cannot achieve. In simple terms: braiding provides robustness, while measurements provide flexibility. Together, they unlock the full computational toolbox.
The Breakthrough Study
The team behind this new research combined large-scale simulations with theoretical analysis. Here’s what they achieved:
- Two-qubit Bell states: These are the simplest entangled states, crucial for quantum communication and teleportation.
- Five-qubit GHZ states: A more complex form of entanglement useful for quantum networks and error correction.
- Random circuits with 10 qubits: Demonstrating scalability, even under disorder, with fidelity above 99%.
What makes this remarkable is not just the success rate, but the fact that it holds up under realistic conditions where imperfections exist.
Why This Matters for the Future of Quantum Computing
1. Restoring Universality
In quantum computing, universality means being able to perform any possible quantum operation. Before this breakthrough, braiding-based quantum computers lacked universality when scaling beyond two qubits. Adding projective measurements changes that, making these systems fully universal.
2. Scalability
The ability to simulate 10 qubits with high fidelity shows that this approach is not just theoretical but has real potential for scaling up to practical quantum processors.
3. Fault-Tolerance
Noise and disorder are among the biggest challenges in building quantum machines. Because topological quantum computing is naturally resistant to errors, and because measurements add control, this hybrid method provides both robustness and versatility.
4. Broad Applications
This could transform fields such as:
- Cryptography: Enabling secure communications through quantum key distribution.
- Drug discovery: Simulating complex molecules faster than classical computers.
- Artificial intelligence: Training models with computational resources far beyond today’s limits.
- Finance: Optimizing complex portfolios with thousands of variables.
A Step-by-Step Guide to How It Works
Step 1: Encode Qubits Using Anyons
Qubits are stored in the state of anyons within a two-dimensional system, such as quantum Hall states or topological superconductors.
Step 2: Perform Braiding Operations
Anyons are moved around each other in specific patterns, creating transformations in the quantum state that are highly resistant to errors.
Step 3: Apply Projective Measurements
Strategic measurements collapse qubits into useful states or switch between different encoding schemes. This expands the available gate set.
Step 4: Combine for Universality
Together, braiding and measurement allow researchers to implement the full set of universal quantum gates.
Step 5: Scale Up
By repeating the process across multiple anyons and qubits, the method scales to larger systems with high fidelity.
Challenges Ahead
While the results are promising, several challenges remain before this approach can be put into practice:
- Experimental Realization: Simulations are powerful, but real-world experiments with anyons are still in their early stages.
- Material Engineering: Creating stable topological systems (e.g., Majorana zero modes) requires cutting-edge materials science.
- Measurement Precision: Implementing reliable projective measurements at scale is not trivial.
- Integration with Other Platforms: Combining this approach with existing quantum hardware may require new hybrid architectures.
Breakthrough: Scientists Unlock Universal Quantum Computing With Exotic Anyons
Want to Join the Future of Quantum Computing? Qiskit Advocate Applications Now Open
Aegiq and Pixel Photonics Team Up to Supercharge Scalable Quantum Computing
FAQs About Projective Measurements Unlock New Power in Quantum Computing With Anyon Braiding
Q1: What makes anyons different from regular particles?
Anyons exist only in two-dimensional systems and have unique exchange properties. When braided, their quantum state changes in a way that depends on the path, unlike bosons or fermions.
Q2: Why isn’t braiding alone enough for universal quantum computing?
Braiding operations can’t generate every possible quantum gate, especially as the system scales. This limits universality beyond two qubits.
Q3: How do projective measurements fix this?
Measurements collapse the system into specific states, allowing researchers to switch encodings and access operations otherwise unavailable through braiding.
Q4: Are projective measurements destructive?
Not in this context. Instead of being a drawback, the collapse is used strategically to expand computational power.
Q5: How soon could we see real-world implementations?
While theoretical progress is strong, experimental platforms like Majorana-based superconductors or quantum Hall systems need further development before this approach can be fully realized.