Quantum computing is an extraordinary frontier of science that promises to revolutionize technology by solving complex problems far beyond the reach of classical computers. Recently, scientists have successfully demonstrated topological strong zero modes on superconducting processors, a pioneering step that could drastically enhance the stability and power of quantum computers. But what exactly are these topological strong zero modes, and why is this discovery so crucial? This article breaks down the concept, its significance, and practical implications in a way that anyone can understand—while also providing detailed insights for professionals and enthusiasts.

Table of Contents
What Are Topological Strong Zero Modes?
At the heart of this breakthrough are topological strong zero modes, special quantum states that exist on the edges of certain quantum materials. Unlike ordinary quantum bits (qubits), which are fragile and prone to environmental noise (called decoherence), these zero modes enjoy enhanced protection because of their topological nature. Topology is a branch of mathematics dealing with properties that remain unchanged even when objects are stretched or twisted without tearing. In quantum materials, this translates to states that are resistant to disturbances.
To put it simply, topological strong zero modes can be thought of as robust guardians of quantum information. They “lock” the information in a special way so that local errors or fluctuations don’t easily destroy it. This protection is vital for building reliable quantum computers capable of performing long and complex calculations.
Why Use Superconducting Processors?
Superconducting processors are one of the leading physical platforms for quantum computing. They use tiny circuits cooled to near absolute zero to create, manipulate, and read out qubits. Superconductors allow electrical currents to flow without resistance, helping maintain delicate quantum states longer than many other types of quantum hardware.
The successful demonstration of these topological modes on superconducting processors bridges theoretical predictions and practical realizations, indicating that existing quantum hardware can be enhanced for better performance using topological principles.
Scientists Demonstrate Topological Strong Zero Modes on Superconducting Processors
| Feature | Description |
|---|---|
| What is demonstrated? | Topological prethermal strong zero modes on superconducting quantum processors. |
| Significance | Long-lived quantum information despite thermal noise, paving the way for robust quantum memories and fault-tolerant quantum computing. |
| Qubit type | Topological qubits encoded in edge modes, protected by emergent symmetries rather than local order. |
| Hardware | Programmable superconducting qubit array (around 100 qubits) used to simulate a disorder-free one-dimensional Hamiltonian. |
| Benefits over conventional qubits | Immune to many local errors and decoherence, stable at finite temperatures, enabled by symmetry protection. |
| Future potential | Enables scalable, stable quantum memories and error correction approaches critical for quantum networks and computing. |
Scientists’ demonstration of topological strong zero modes on superconducting processors marks a pivotal moment in quantum computing. By successfully encoding and preserving quantum information in edge modes that are protected by topological properties and emergent symmetries, they have overcome significant barriers in qubit stability and error resistance. This breakthrough not only advances the theoretical understanding of topological quantum matter but also provides a practical roadmap toward building scalable, robust quantum computers and networks.
As research continues to explore these modes’ full potential, integrating them with existing quantum architectures could soon pave the way for fault-tolerant quantum systems capable of tackling problems classical computers can’t solve.
Practical Guide to Understanding Topological Strong Zero Modes
The Basics: Quantum Bits and Decoherence
In classical computing, information is stored as bits represented by 0s and 1s. Quantum computers use qubits, which can be 0, 1, or both simultaneously (superposition). Qubits are also entangled, meaning their state depends on each other even over distance, enabling powerful parallel computations.
However, quantum states are very fragile; decoherence from noise, temperature fluctuations, or measurement can destroy qubit information quickly. Protecting qubits to preserve coherence is the biggest challenge holding back practical quantum computers.
What Makes a Quantum State Topological?
Topology protects quantum states by embedding information in global properties of a system rather than local ones. Imagine a coffee cup made of soft rubber being reshaped into a donut without cutting—it remains topologically the same because it has one hole. In quantum systems, information encoded in such “topological features” cannot be altered easily by small, local errors.
Strong Zero Modes and Their Role
Strong zero modes are special quantum states localized at the edges of certain materials. They commute approximately with the system’s energy operator (Hamiltonian), which means they remain stable and persistent for a long time, even during thermal agitation. This property allows them to serve as logical qubits with extended lifetimes, crucial for quantum memory and computation.
Experimental Demonstration Steps
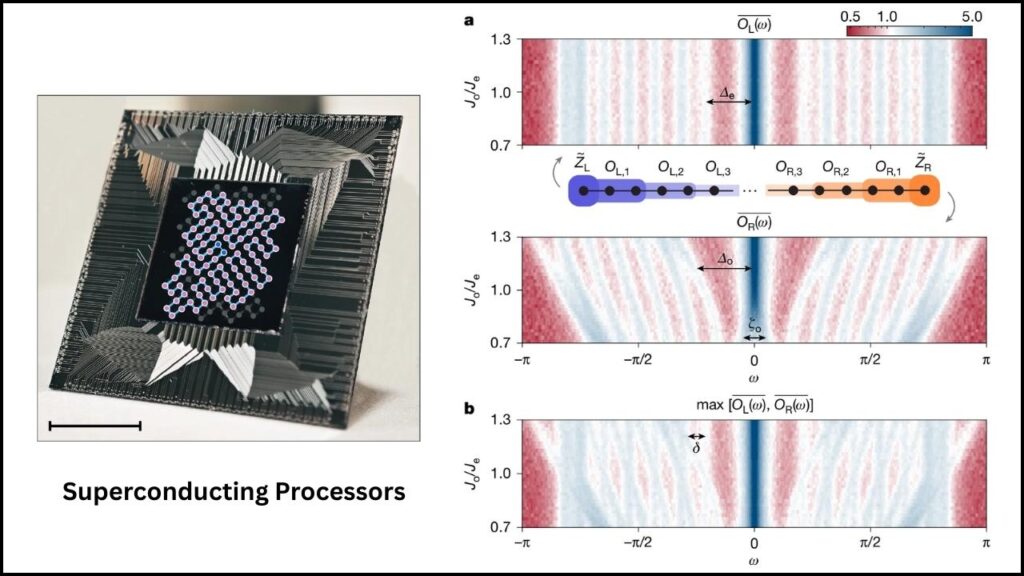
- Creating a Model System: Researchers programmed about 100 superconducting qubits to simulate a specific one-dimensional quantum system with tailored couplings (interactions between qubits).
- Initializing Topological Edge Modes: Using precise quantum gate operations, they initialized logical Bell states—entangled quantum states localized at the system’s edges that represent the topological modes.
- Testing Stability Across Time: The team observed the persistence of these modes over many cycles (up to 30), checking for decoherence and loss of quantum states.
- Tuning the System: By changing the coupling patterns (uniform or dimerized chains), they analyzed how symmetry affects the robustness of the topological modes.
- Observing Coherence at Finite Temperatures: The key success was maintaining stable edge modes without requiring the system to be at near absolute zero, a significant practical advantage.
Importance for Quantum Computing and Industry
The demonstration confirms that topological qubits could be integrated into current superconducting quantum computers, providing a natural form of error resistance without the extreme overhead of traditional error correction. This development is expected to:
- Reduce Error Rates: Topological qubits can theoretically achieve error rates as low as 10−610−6, far below today’s typical physical qubits needing heavy error correction.
- Enhance Qubit Lifetimes: Because of symmetry protection, qubit coherence times can be extended beyond conventional expectations, enabling longer, more complex quantum computations.
- Accelerate Quantum Memory Development: Stable quantum memories are pivotal for scalable quantum networks and quantum communication protocols.
- Bridge Theory and Experiment: The experimental results validate decades of theoretical work, creating a solid foundation for future quantum hardware improvements.
Researchers Uncover Hidden Mysteries of High-Temperature Superconductors: A Comprehensive Guide
New Quantum Weirdness Spotted in Superconductor—Could It Upend Physics?
Antiferromagnetic Tunnel Junctions Could Power Next-Gen Spintronics Revolution
FAQs About Scientists Demonstrate Topological Strong Zero Modes on Superconducting Processors
Q1: What is the difference between a regular qubit and a topological qubit?
Regular qubits are encoded in local physical states and are highly vulnerable to noise and decoherence. Topological qubits encode information in system-wide topological properties, providing intrinsic protection against many errors.
Q2: How does a superconducting processor benefit quantum computing?
Superconducting processors, cooled to extremely low temperatures, offer fast and reliable control of qubits via microwave circuits. They’re among the most advanced quantum hardware available, used by companies like IBM and Google.
Q3: Why is maintaining coherence at finite temperature important?
Most current quantum experiments require ultracold temperatures close to absolute zero, which is costly and hard to maintain. Finite temperature coherence means quantum devices will be more practical and scalable.
Q4: Can these topological states be used for actual quantum computing tasks now?
While promising, this is still an early step. The demonstrated robustness shows potential for future practical quantum memories and qubit designs that could be integrated with active error correction schemes.